top of page
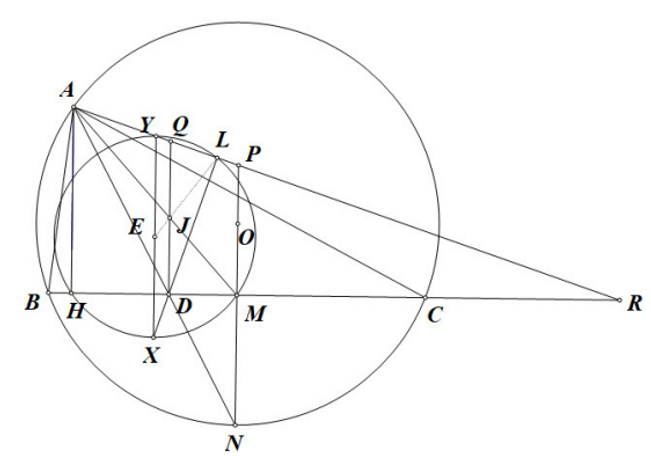
P3: Given ABC inscribed in (O) and bisector BD. M is the midpoint of BC. J is a point on AM such that JD is perpendicular to BC. Prove that (J, JD) and Euler-circle touch.

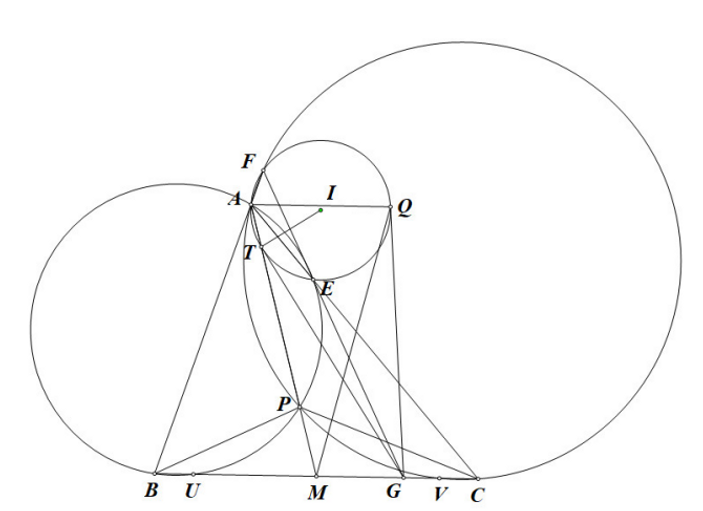
P4: Given triangle ABC. P is an arbitrary point on the median AM. (APB) intersects AC at E. (APC) intersects AB at F. EF intersects BC at G. (AEF) intersects AM at T. Prove that TG touches (AEF).

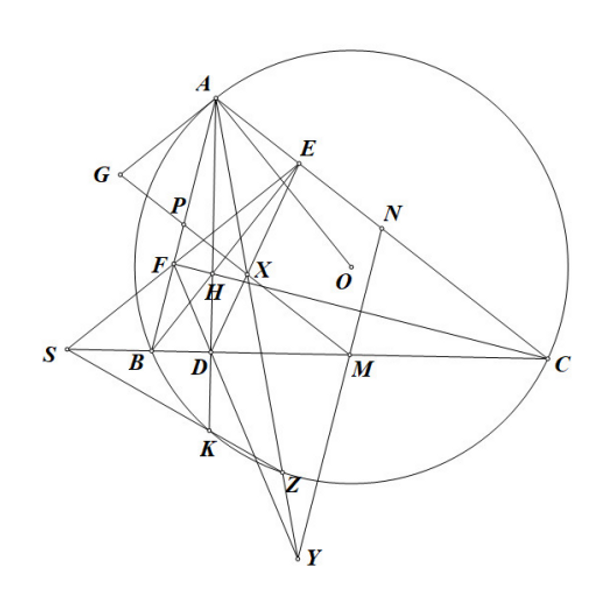
P6: Given ABC inscribed in (O) with the orthocenter H. M,N,P are respectively midpoints BC,CA,AB. AD,BE,CF are, respectively, heights of triangle ABC. K is the reflection of H through BC. DE intersects MP at X and DF intersects MN at Y. XY intersects arc BC at Z. Prove that K,Z,E,F lies on one circle.

bottom of page