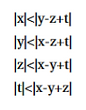Counterproof and inequality
There are many ways to prove inequalities, such as changing new variables or using equivalent transformation. There is also a famous way: using counter-proof.
There are some examples that I will now show you:
Example:
Given real numbers a,b,c such that: a+b+c > 0, ab+bc+ca > 0, abc > 0. Prove that a,b,c are positive numbers.
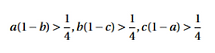
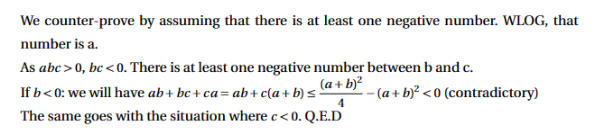
Or another example:
Given real positive number a,b,c (a,b,c<1). Prove that: at least one among the three inequalities is wrong:
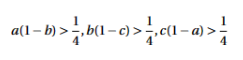

The question here is when to use counter-proof. In some problems, there are some states that prove that at least one of something has to satisfy something or prove that everything satisfies something. You should use counter-proof as it will give you the real information from the statement that the problem needs us to prove.
There is also one problem from the Moscow Olympiad:
Solve the set of inequalities: